Stress thermique en endurance – Echanger

Dans la partie 1 de l’article, il était question de la production de chaleur interne par le métabolisme, qu’on avait noté M. Comme il l’avait été expliqué dans ce premier article (et rappelé avec l’équation 1), l’évolution de la température interne est également influencée par la chaleur échangée avec l’extérieur Qext (la chaleur que l’on capte, et la chaleur que l’on dissipe).

Les mécanismes de transfert thermique

On distingue classiquement trois modes de transfert thermique. En réalité, on peut les regrouper en deux grandes familles : d’une part, le transfert thermique qui se propage sans support matériel, autrement dit le rayonnement, et d’autre part, celui qui se propage au sein de la matière. Dans cette seconde catégorie, on distingue la conduction, lorsque la matière est immobile (solide ou fluide au repos), et la convection, lorsqu’un fluide est en mouvement, comme l’air.

À partir de là, le corps humain dissipe de la chaleur selon quatre mécanismes :

• La conduction : l’énergie thermique se propage de proche en proche dans un milieu solide. En course à pied, cela concerne les échanges entre la peau et les vêtements, ou entre la chaussure et le sol. Ce mode de transfert reste très faible par rapport aux autres et ne sera donc pas détaillé davantage.
• La convection : L’énergie se déplace de proche en proche dans la matière en mouvement, typiquement l’air ambiant. Le transfert de chaleur entre la peau et l’air est d’autant plus efficace que la vitesse de l’air est élevée.
• Le rayonnement : ici, la chaleur est émise sous forme d’ondes électromagnétiques, sans besoin de support matériel. Ce mode de dissipation est prédominant au repos.
• L’évaporation : bien qu’elle implique un fluide en mouvement, on la distingue de la convection car elle résulte d’un changement d’état (passage de l’eau de la sueur à la vapeur). Lors d’un effort physique, c’est le principal mode de dissipation de la chaleur.

Q_ext s’écrit alors de la façon suivante :

avec Q_cond la chaleur échangée par conduction, Q_conv la chaleur échangée par convection,  Q_evap la chaleur échangée par évaporation et Q_ray la chaleur échangée par rayonnement. Ces termes sont positifs si la chaleur est reçue, et négatifs si elle est dissipée. Le terme lié à l’évaporation est toujours négatif puisque le corps ne reçoit pas de chaleur par évaporation.

La quantité de chaleur reçue et dissipée par le corps dépend directement des conditions extérieures. Par exemple, la chaleur reçue par rayonnement sera plus importante en plein soleil que sous un ciel nuageux. De même, la dissipation par convection sera renforcée en présence de vent. Les vêtements jouent également un rôle clé dans ces échanges, en fonction de leur matière et de leur couleur, qui influencent à la fois l’absorption de chaleur et la capacité à la dissiper. Comprendre l’interaction entre ces différents facteurs permet de faire des choix plus éclairés en matière de tenue, de stratégie de refroidissement et de plan de course, afin de limiter au maximum l’élévation de la température corporelle et, par conséquent, la baisse de performance.

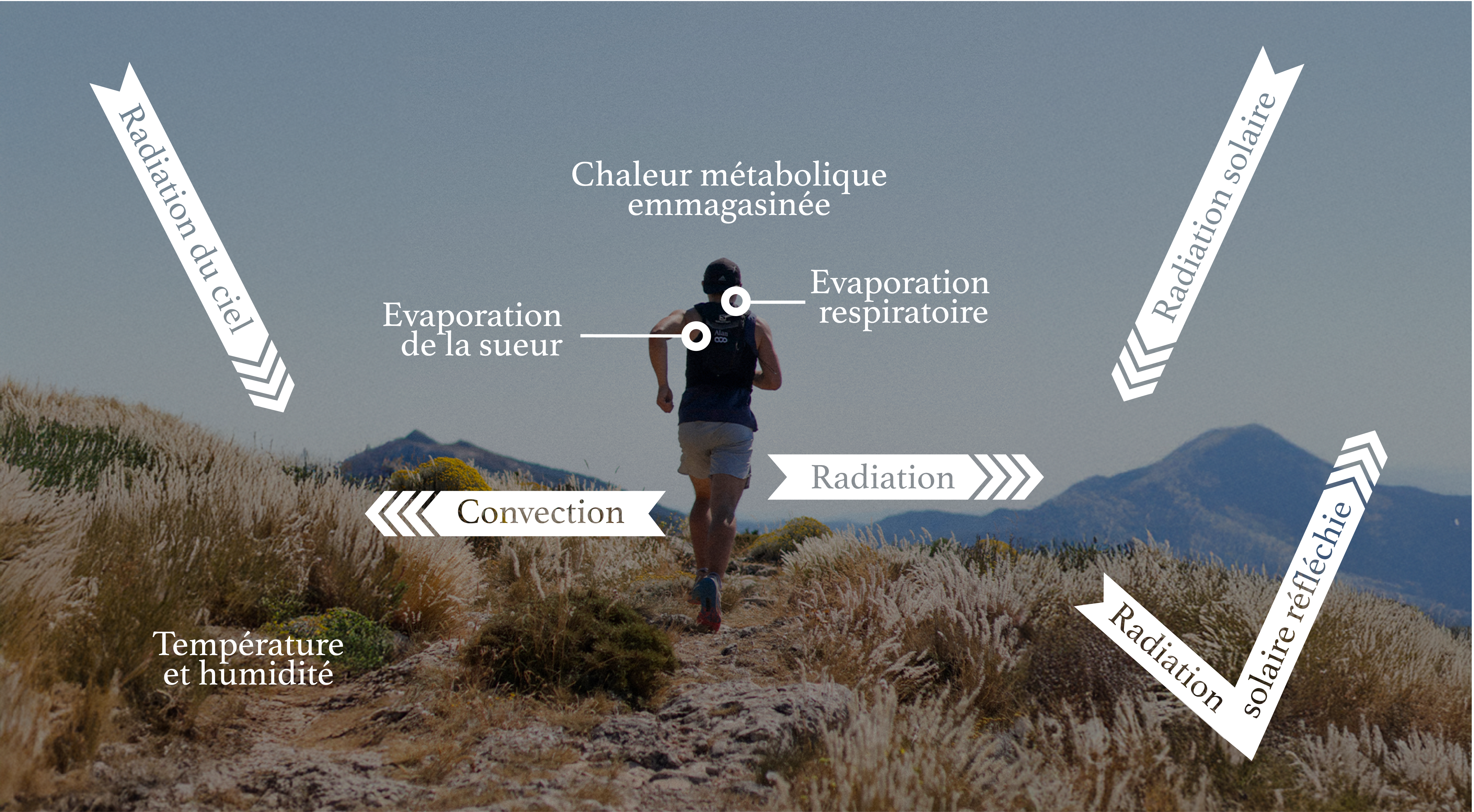
Figure 1 : Illustration des différents modes de transferts thermiques présents lors d’un effort physique, inspiré de [1]

Dissipation de chaleur par convection

Formule générale et paramètres 

Ce mode de transfert de chaleur est le deuxième plus efficace pour dissiper la chaleur lors d’un effort physique (après l’évaporation). Celui-ci dépend de la différence de température entre la peau et celle de l’air extérieur. Pour mieux comprendre, la puissance thermique échangée par convection s’écrit de la façon suivante (d’après [4]) :

h_c est le coefficient d’échange par convection et s’exprime en W/(m².K). Il représente la puissance échangée par unité de surface dans le cas d’une différence de température de 1 °C.

Dans le cadre d’une activité physique telle que la course à pied ou le vélo, la convection est supposée forcée (par opposition à la convection naturelle, voire Note ci-dessous). Cela implique que le coefficient de convection, et donc la chaleur échangée par convection, dépend des paramètres suivants :

• les propriétés de l’air, qui changent en fonction de la température et de l’altitude 
• la morphologie de la personne, qui va avoir un impact sur la surface d’échange entre autre
• la vitesse relative de l’air, que l’on notera w_r pour la suite

Dans des conditions environnementales données, et pour un profil d’individu donné, le coefficient de convection peut s’écrire d’après [1] :

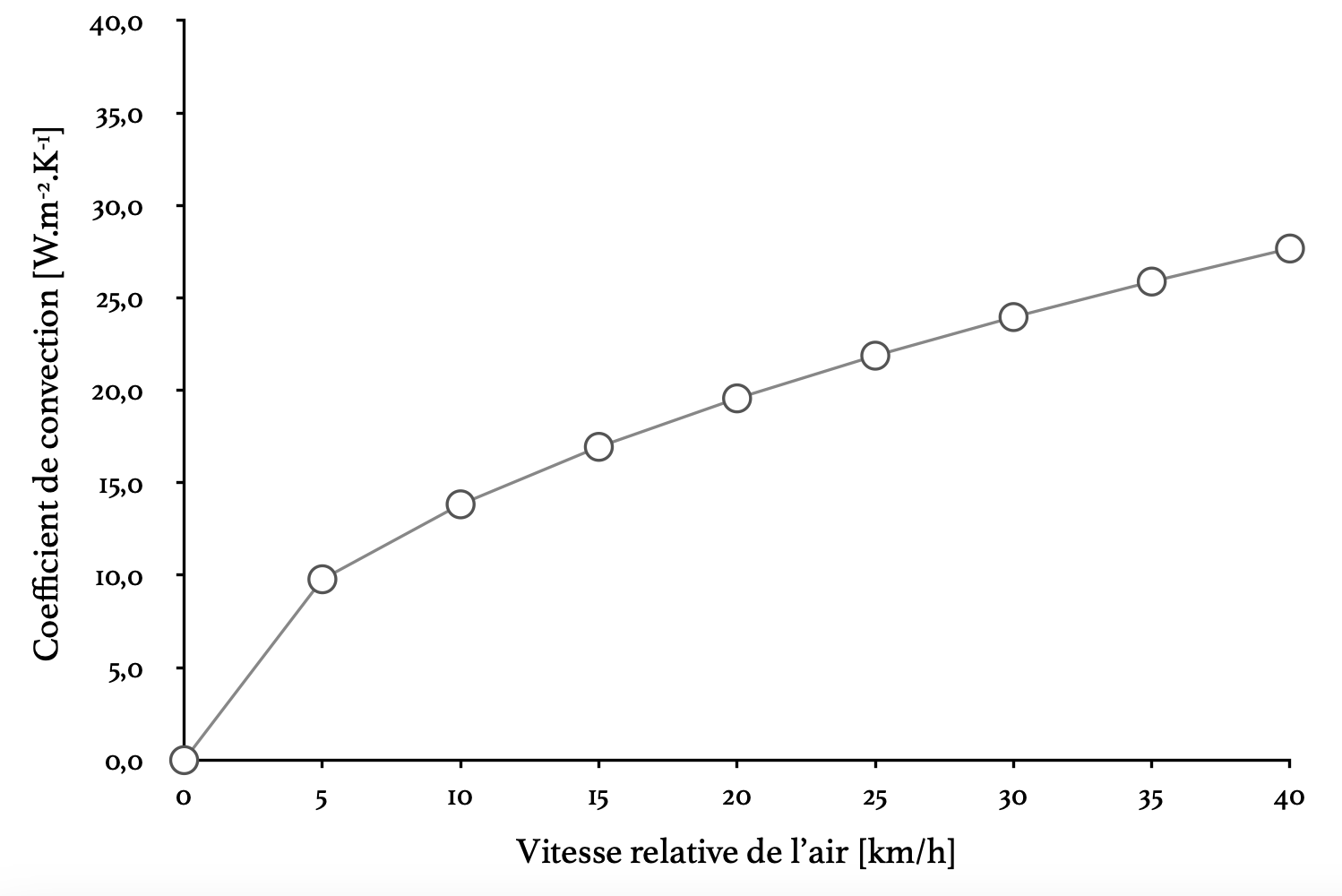
Figure 2 : Évolution du coefficient de convection en fonction de la vitesse relative de l’air, d’après l’équation 4

Finalement, l’expression de [math]\dot{Q}_{conv}[/math] permet de voir que la chaleur échangée par convection sera d’autant plus grande que le vent sera important, que la différence entre la température de la peau et la température de l’air sera importante et que la surface d’échange sera grande. Une vitesse relative de vent qui double va multiplier par 1,4 la chaleur échangée par convection (pour une différence de température donnée).

De même que pour la conduction, l’expression montre que si la température de peau est inférieure à la température de l’air, alors le corps ne dissipera pas mais emmagasinera de la chaleur par convection ([math]\dot{Q}_{conv}[/math] < 0).

Influence du milieu

Même si la vitesse du vent influence clairement le coefficient d’échange convectif h_c​, le milieu dans lequel on évolue joue également un rôle déterminant. En course à pied ou à vélo, l’athlète est en contact avec l’air ambiant. Mais ce n’est pas le cas des triathlètes lors de la première épreuve, la natation. Pour illustrer la différence de dissipation thermique par convection dans l’air et dans l’eau, comparons la chaleur dissipée dans deux situations : de l’air en mouvement et de l’eau statique.

Données d’entrée :

• Athlète de 1,80 m
• Température du fluide (air ou eau) : 20 °C
• Vitesse de l’air : 20 km/h

Les coefficients de convection obtenus sont alors les suivants :

• h_c,air = 10,65 W.m^-2.K^-1 (convection forcée)
• h_c,eau = 132,00 W.m^-2.K^-1 (convection naturelle)

Autrement dit, même sans mouvement de l’eau, le corps dissipe 13 fois plus de chaleur lorsqu’il est immergé que lorsqu’il est exposé à de l’air en mouvement. C’est énorme ! En cas de coup de chaud pendant une course, une immersion totale dans l’eau est sans doute l’un des moyens les plus efficaces pour faire baisser rapidement la température corporelle.

Echange de chaleur par radiation

Explication du phénomène de rayonnement thermique

Tout objet dont la température est supérieure à 0 kelvin (soit -273,15 °C) émet en permanence des ondes électromagnétiques qui se propagent dans l’espace à la vitesse de la lumière. Ce phénomène est à l’origine du rayonnement thermique. Les photons émis peuvent exciter les particules des surfaces qu’ils atteignent, ce qui entraîne une élévation de température. Le rayonnement thermique pouvant se propager dans le vide, c’est par ce seul moyen que le Soleil transmet son énergie à la Terre.

Le rayonnement thermique émis par un corps du fait de sa température se situe dans une gamme de longueurs d’onde allant d’environ 0,1 à 100 micromètres. Comme on peut le voir sur la figure ci-dessous, un corps humain, dont la température avoisine 300 K, émet principalement dans l’infrarouge. En revanche, le rayonnement solaire est réparti entre l’ultraviolet, le visible (où se situe son pic) et l’infrarouge. C’est pour cela que le rayonnement émis par le corps humain est invisible à l’œil nu, contrairement à celui du Soleil.

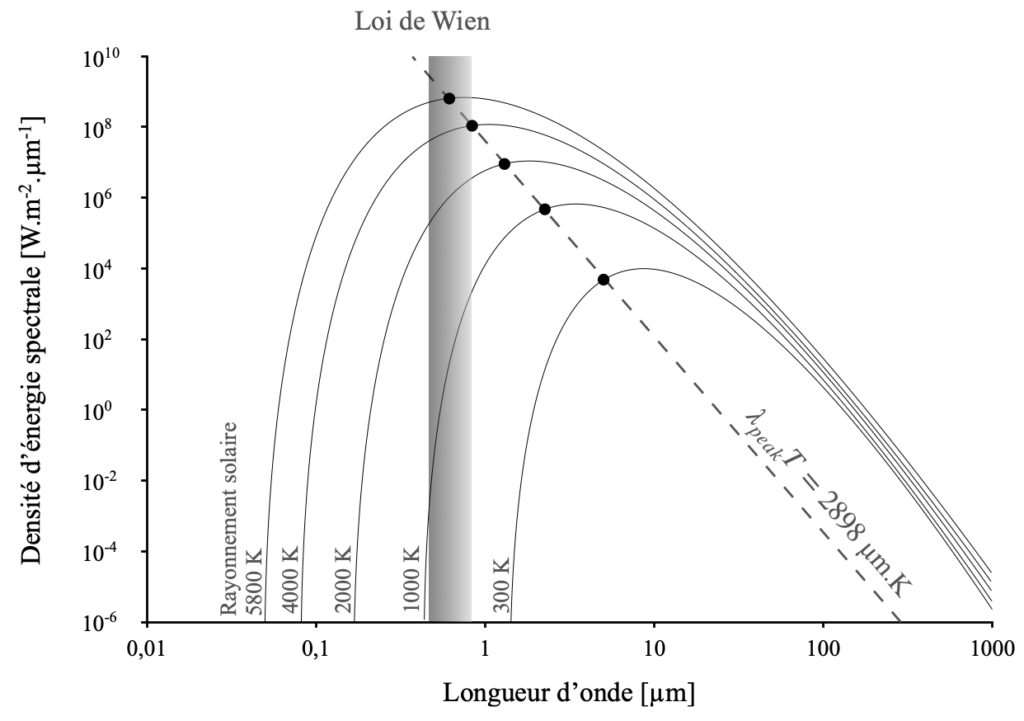
Figure 3 : Intensité de radiation pour différentes températures et Loi de Wien 

La puissance thermique émise par un corps, c’est à dire la quantité d’énergie émise par seconde par un corps à une température T est définie par la relation de Stefan-Boltzmann:

où [math]\sigma[/math]=5,67.10-8 W.m^-2.K^-4 est la constante de Stefan–Boltzmann, et est l’émissivité (voir note ci-dessous). A la température de la peau (34 °C), l’émission thermique est de 505 W.m^-2 pour [math]\epsilon[/math]=1. On peut voir dans cette relation que la température est à la puissance 4. Ce qui signifie qu’un corps 2 fois plus chaud, émettra 16 fois plus de puissance thermique sous forme de rayonnement.

Application au corps humain

Si on revient au corps humain, on comprend maintenant que le corps va dissiper de l’énergie par rayonnement, mais aussi et surtout en capter de l’extérieur, notamment par le soleil, le ciel, le sol et les murs. Plus précisément, d’après [1] et [4], il est possible d’identifier six termes de rayonnement. 

Plus précisément, d’après [1] et [4], on peut distinguer six composantes du rayonnement affectant l’organisme :

• Trois composantes solaires (principalement dans le visible et le proche infrarouge) :

• le rayonnement direct du soleil,
• le rayonnement diffus, diffusé par l’atmosphère et les nuages,
• le rayonnement réfléchi par le sol ou d’autres surfaces (albédo).

• Deux composantes thermiques (IR) :

• le rayonnement infrarouge descendant du ciel,
• le rayonnement ascendant émis par le sol.

• Enfin, le rayonnement thermique émis par le corps lui-même, proportionnel à sa température de surface.

Ainsi, d’après [1], la chaleur emmagasinée par le corps provenant du rayonnement de l’environnement extérieur peut être estimée avec la relation suivante :

[math]\dot{Q}_{S,D}[/math], [math]\dot{Q}_{S,I}[/math], [math]\dot{Q}_{S,R}[/math] représentent respectivement le rayonnement solaire direct, indirect et réfléchie sur le sol. [math]\dot{Q}_{IR,U}[/math] et [math]\dot{Q}_{IR,D}[/math] représentent le rayonnement thermique (dans l’infrarouge) qui remonte du sol (U pour up) et qui descend du ciel (D pour down). représente le coefficient de réflectivité et le coefficient d’absorption. Le premier indique la part du rayonnement renvoyée par la surface, tandis que le second exprime la part absorbée. Une surface claire et brillante aura un fort pouvoir réfléchissant ( proche de 1), tandis qu’une surface sombre absorbera davantage de rayonnement et chauffera plus rapidement.

Cette relation est intéressante pour comprendre la décomposition physique des sources radiatives dans l’environnement. Cependant, elle est difficile à appliquer sur le terrain, car chaque terme nécessite des mesures directionnelles et spectrales précises. En pratique, on préfère utiliser une formulation intégrée, qui regroupe tous ces flux dans un terme unique : la température radiante moyenne T_r, mesurée avec un globe noir. Cela mène à une autre forme du flux radiatif net échangé par le corps qui s’écrit d’après [4] :

avec T_r la température radiante moyenne et h_r le coefficient d’échange thermique par rayonnement. hr s’écrit, toujours d’après [4] :

où :

• A_r/A_D ≈ 0,71 pour une personne debout 
• f_cl : facteur d’augmentation de surface lié aux vêtements, qui correspond au rapport entre la surface externe des vêtements et la surface corporelle nue. Il reflète l’augmentation apparente de surface d’échange par rayonnement à cause du volume ou du gonflement des vêtements. Il vaut donc au moins 1 pour une personne nue. 
• [math]\sigma[/math] et [math]\varepsilon[/math] respectivement la constante de Stefan-Boltzmann et l’émissivité de la surface corporelle, déjà introduis précédemment.

Impact des vêtements

Contrairement aux rayonnements infrarouges, les rayons du domaine visible (rayonnement solaire) peuvent être partiellement réfléchis, notamment en fonction de la couleur des surfaces. La couleur des vêtements a donc un impact non négligeable sur la quantité d’énergie absorbée par rayonnement.

Prenons un exemple pratique à partir de l’équation 6, afin de comparer l’influence de la couleur des vêtements sur la quantité de chaleur absorbée par rayonnement. le coefficient (1-) représente la part du rayonnement solaire qui n’est pas réfléchi par la surface (peau ou vêtement). Selon [1], la réflectivité de la peau dans le visible est d’environ 0,3 ; celle des vêtements noirs est d’environ 0,2, tandis que celle des vêtements blancs atteint 0,88. En supposant que les vêtements couvrent 50 % de la surface corporelle, on obtient une réflectivité moyenne :

• Pour des vêtements blancs : [math]\rho=0,50,3+0,50,88=0,59[/math]

• Pour des vêtements noirs : [math]\rho=0,50,3+0,50,2=0,25[/math]

Cela signifie que dans le premier cas, le corps absorbe 41 % du rayonnement solaire, contre 75 % dans le second. 

Sur la durée d’une épreuve d’ultra-endurance, cette différence peut entraîner une accumulation thermique importante, que le corps devra compenser par une évaporation accrue (transpiration) et un effort de thermorégulation. Un choix judicieux de la couleur des vêtements peut donc contribuer à limiter le stress thermique, surtout en conditions ensoleillées.

En pratique, toute l’énergie absorbée par les vêtements n’est pas transférée directement au corps. Une partie est stockée dans les vêtements eux-mêmes, ce qui élève leur température. On y reviendra dans une partie dédiée plus loin dans l’article.

Ces calculs sont seulement des ordres de grandeur, mais ils illustrent bien à quel point le choix du textile peut influencer la charge thermique en conditions chaudes. Sur une course longue, cet impact peut clairement faire la différence — des athlètes comme Kristian Blummenfelt aux Jeux de Tokyo l’ont parfaitement compris.

Dissipation de chaleur par évaporation

Comment fonctionne l’évaporation

Lors d’un effort physique, l’évaporation est le mécanisme de dissipation de chaleur le plus efficace, mais aussi l’un des plus mal compris, car plus complexe qu’il n’y paraît.

L’évaporation intervient à deux niveaux : au niveau de la respiration et au niveau cutané. Le second constitue clairement le mode dominant. En effet, lors d’un effort physique, la part de chaleur dissipée par la respiration devient négligeable comparée à celle évacuée par la peau (voir équations 6 et 7 de la partie 1).

Pour évacuer la chaleur, le corps produit de la sueur via les glandes sudoripares. Lorsqu’elle s’évapore, cette sueur absorbe de l’énergie thermique provenant du corps pour passer de l’état liquide à l’état gazeux. Cette énergie, nécessaire au changement d’état, est appelée chaleur latente de vaporisation. Elle dépend de la température. Tout le monde sait que l’eau bout à 100 °C, ce qui correspond à une vaporisation par ébullition. Heureusement, la sueur ne chauffe évidemment pas à ce point sur la peau. Dans notre cas, il s’agit d’un autre type de transformation : l’évaporation. Ce dernier est un processus lent et superficiel qui se produit à toutes les températures (voir la note pour plus de détails).

Notion d’humidité relative

Lorsque l’on parle d’évaporation, une notion clé à prendre en compte est celle de l’humidité relative. Celle-ci correspond à la quantité d’eau contenu dans l’air sous forme de vapeur. Elle peut s’exprimer avec la relation suivante :

La quantité d’eau que l’air peut contenir est fixée par la pression de vapeur saturante de l’eau. Plus de l’eau s’évapore dans un l’air, plus sa quantité dans l’air augmente et plus la pression partielle de la vapeur d’eau [math]P_{vap}[/math] dans l’air augmente. A un moment, l’air ne peut plus contenir davantage d’eau : on a atteint la pression de vapeur saturante [math]P_{vap,sat}(T)[/math] et l’ humidité relative vaut 100 %. Comme il est possible de le voir dans la formule ci-dessus, la pression de vapeur d’eau saturante dépend de la température. Plus la température est élevée, plus la pression de vapeur d’eau saturante est élevée, et plus l’air peut contenir de l’eau sous forme de vapeur. C’est notamment ce qui explique le phénomène de rosée la nuit quand la température diminue, et qui disparaît le matin quand la température augmente.

Pour en revenir à l’évaporation de la sueur, on comprend maintenant que le taux d’humidité de l’air va avoir un impact crucial sur la capacité du corps à faire évaporer la sueur, et ce qu’il faut bien comprendre, c’est que si la sueur ne s’évapore pas, la chaleur ne se dissipe pas.

Calcul de la chaleur dissipée par évaporation

La puissance thermique dissipée par évaporation peut être calculée par la relation suivante d’après [2] :

avec [math]\dot{m}[/math] le débit massique de sueur en gramme par seconde, la chaleur latente de vaporisation de l’eau (2,454 kJ/g) expliquée dans le premier paragraphe de cette section. En pratique, la chaleur évacuée par évaporation peut être facilement évaluée en mesurant simplement la perte hydrique, en se pesant avant et après une session, et en appliquant ensuite la formule de l’équation 10.

Savoir quelle quantité de chaleur a été évacuée par la transpiration, ou au moins estimer la masse d’eau perdue, peut être très intéressant — notamment dans le cadre d’un bloc d’entraînement en conditions chaudes, afin de mesurer l’amélioration de l’efficacité du mécanisme d’évaporation. Il est également pertinent de pouvoir estimer la capacité maximale d’évaporation dans des conditions environnementales données, notamment en fonction de l’humidité et de la température ambiante. Cela permet de déterminer si l’évaporation sera le principal mécanisme de dissipation thermique ou s’il faudra recourir à d’autres stratégies. Cela permet aussi de quantifier l’impact de l’humidité sur la capacité maximale du corps à évacuer la chaleur par évaporation.

D’après [3] équation 1.14, cette capacité maximale s’écrit :

avec [math]P_{vap}[/math] la pression partielle de vapeur dans l’air, [math]P_{skin,sat}[/math] la pression de vapeur saturante à la surface de la peau, et [math]h_e[/math] le coefficient de transfert par évaporation qui se détermine via la relation de Lewis qui s’écrit au niveau de la mer [2] :

La première chose que cette équation permet de comprendre c’est que plus l’air est humide (ie : [math]P_{vap}[/math] est grand, ie : l’humidité relative est importante), plus [math]\dot{Q}_{evap,max}[/math] est petit, ou autrement dit, moins le corps peut dissiper la chaleur par évaporation.

La deuxième chose que l’on remarque, c’est que le coefficient de transfert par évaporation est proportionnel au coefficient de convection, lui-même dépendant de la vitesse relative du vent (voir section sur la convection). Plus le vent est fort, plus la dissipation thermique par évaporation devient efficace. Cela s’explique par le fait qu’un vent plus soutenu renouvelle plus rapidement l’air saturé en vapeur d’eau au contact de la peau, remplacée par de l’air plus sèche, ce qui favorise l’évaporation.

Le paradoxe sur l’influence du textile

Lorsque l’on s’intéresse aux transferts thermiques entre le corps et l’environnement extérieur, il apparaît un paradoxe. En effet, comme on a pu le voir dans la partie sur le rayonnement, le fait de se couvrir davantage avec des vêtements blancs va permettre de réduire la chaleur captée par rayonnement. Cependant d’un autre côté, le fait de se couvrir va considérablement réduire la dissipation de la chaleur par évaporation et convection. L’enjeu est donc de savoir s’il vaut mieux limiter la quantité de chaleur captée par radiation, ou plutôt maximiser la quantité de chaleur dissipée par convection et évaporation. Cela va dépendre des conditions extérieures : humidité, vent, ciel dégagé, etc. 

Les équations présentées jusque-là comparent la température de la peau à celle de l’environnement. Or, dans les zones couvertes, ces échanges sont partiellement bloqués par les vêtements.

Impact sur la convection

Pour les zones habillées, le flux de chaleur convective est réduit proportionnellement à [math]F_{cl}[/math], appelé facteur d’efficacité thermique de Burton pour les vêtements [2]. La puissance thermique dissipée par convection s’écrit alors :

Pour des vêtements légers de sport, [math]F_{cl}[/math] est environ égal à 0,72 (d’après [2]). Pour une personne nue, [math]F_{cl}[/math]=1.

Il est pertinent de rappeler que, lorsque la température extérieure devient supérieure à celle de la peau, la convection ne joue plus un rôle de dissipation, mais devient au contraire une source de gain thermique. Dans ce cas, le port de textile peut limiter cette entrée de chaleur en freinant les échanges convectifs. Là encore, ce choix dépend de la capacité du corps à pouvoir évacuer la chaleur par évaporation.

Impact sur le rayonnement

[math]F_{cl}[/math] ne s’applique pas uniquement à la convection : il réduit aussi l’efficacité des échanges par rayonnement entre la peau et l’environnement. Lorsqu’un vêtement recouvre une surface corporelle, cette surface ne « voit » plus directement le ciel, le soleil ou les objets environnants, et le rayonnement thermique ou solaire incident est en partie bloqué ou réfléchi par le tissu.

Ainsi, l’équation du flux radiatif net devient, à partir de l’équation 7 :

Plus [math]F_{cl}[/math] est faible (plus on porte de vêtement), moins le corps échange de chaleur par rayonnement, que ce soit en gain (rayonnement solaire ou infrarouge du sol/ciel) ou en perte (rayonnement thermique émis par la peau). Cela traduit donc le paradoxe exprimé précédemment qui est que par temps chaud, se couvrir va effectivement réduire le rayonnement capté, mais également réduire les dissipations par convection et évaporation.

Impact sur l’évaporation

Pour ce qui est de l’évaporation, un terme similaire à [math]F_{cl}[/math] est introduit. Il s’agit de [math]F_{pcl}[/math], connu sous le nom de facteur d’efficacité de perméation de Nishi. Il permet de mesurer le passage de la vapeur d’eau à travers les vêtements et est défini comme suit d’après [2].

où [math]h_{ecl}[/math] est l’équivalent thermique de la vapeur d’eau traversant les vêtements et [math]h_{e}[/math] le coefficient de transfert de chaleur par évaporation de la surface de la peau elle-même défini plus haut.

La puissance thermique maximale dissipée par évaporation s’écrit alors :

Pour des vêtements légers de sport, [math]F_{pcl}[/math] est environ égal à 0,87. De même que pour [math]F_{cl}[/math], [math]F_{pcl}[/math]=1 pour une personne nue.

Bilan et bonnes pratiques

Dans cet article, les différents modes de dissipation thermique ont été étudiés séparément afin de mieux comprendre comment chacun est influencé par les conditions extérieures. Comme le suggèrent les équations, aucun de ces mécanismes n’agit de manière isolée : ils interagissent constamment, en fonction de l’environnement et de la production de chaleur interne. Le textile porté à l’effort a également un impact majeur sur la capacité du corps à dissiper la chaleur, à limiter l’absorption du rayonnement solaire, et donc à maintenir une température interne dans une zone « sûre ».

En lien avec le premier article, on peut retenir que les deux leviers les plus efficaces pour limiter l’élévation de la température centrale (et donc préserver la performance en conditions chaudes) sont :

1. Une stratégie de pacing adaptée,
   
2. Le choix des textiles portés,
   
3. Et dans une moindre mesure, les stratégies de cooling (avant et pendant).
   

Il est important de souligner que ces enjeux liés à l’hyperthermie deviennent cruciaux dès que l’effort dépasse une à deux heures, selon les conditions. Dans ce contexte, la gestion de la température corporelle devient probablement le premier facteur limitant de la performance.

Certaines stratégies simples permettent de limiter l’élévation de la température corporelle en prenant en compte les mécanismes de transfert de chaleur :

• Crème solaire : elle peut former une barrière à la surface de la peau et freiner le processus d’évaporation. 
• Casquette : elle réduit significativement la dissipation de chaleur par convection et évaporation au niveau de la tête — une des zones les plus chaudes du corps. En cas de fort ensoleillement, une casquette blanche permet de limiter l’absorption de rayonnement solaire. Dès que le soleil disparaît, l’enlever permet d’améliorer la dissipation thermique.
• Sac à dos en trail : il couvre la partie supérieure du dos, qui est, tout comme la tête, une importante zone de production de chaleur, limitant à la fois l’évaporation et la convection. La couleur du sac (claire de préférence) peut alors avoir un réel impact pour limiter l’augmentation de la température interne.
• Casques aéro en vélo : ils améliorent l’aérodynamisme mais leur conception fermée empêche toute ventilation. En conditions chaudes, il est pertinent de se demander si le gain aérodynamique compense la baisse de performance liée à la surchauffe. Beaucoup pourraient être surpris de la réponse.